Work in progress
Thrust A: Inverse scattering in complex and uncertain media
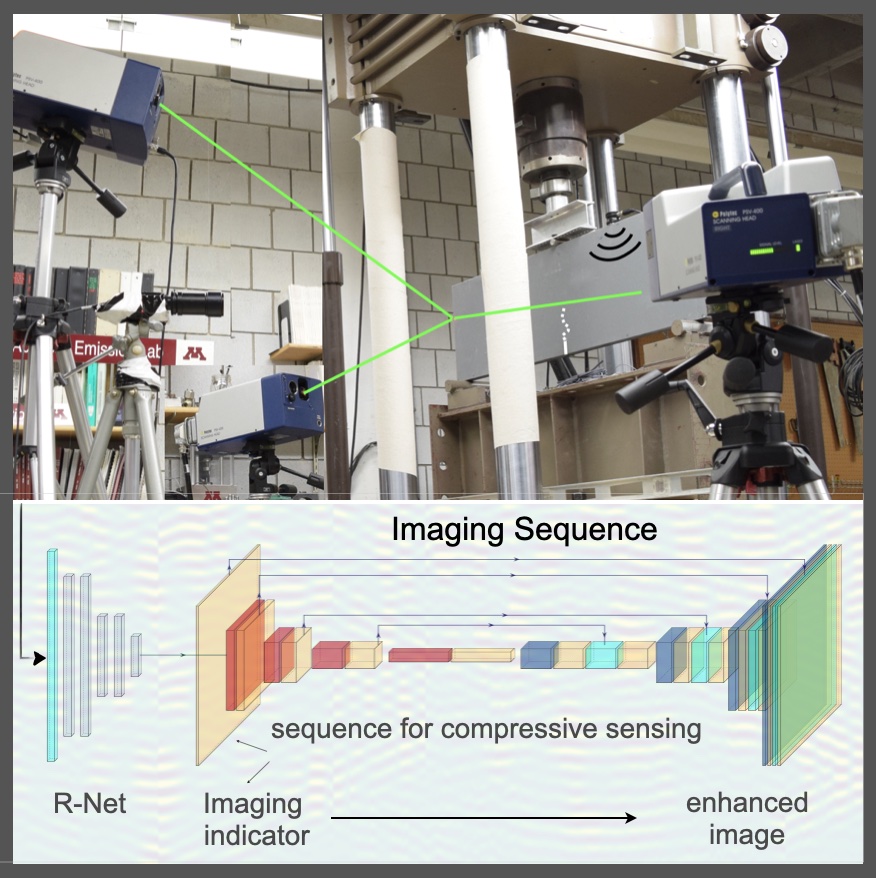
Inverse scattering aims to uncover geometrical and physical properties of hidden objects in a medium from remote observations of scattered waveforms. Intelligent platforms for imaging and characterization in uncertain environments (such as metal printing chambers and energy systems) enable real-time monitoring of additive manufacturing (AM), early anomaly detection in safety-critical components, and efficient energy extraction and storage. Existing approaches, however, often rely on oversimplified assumptions about the background medium, yielding unreliable baseline models. When coupled with partial/one-sided apertures and noisy data, this makes conventional gradient-based waveform inversion brittle, slow, and calibration-intensive. We are developing a mathematically grounded sensing-inference platform for fast spatiotemporal tracking of natural and engineered processes in complex domains. In this vein, we take advantage of advances in sampling approaches to inverse scattering, optimal experimental design, deep learning, and uncertainty quantification. Signature results
-
Differential imaging of advancing fractures in uncertain components — SIIMS, 2020.Establishes the differential evolution indicators for ultrasonic imaging of propagating fractures in specimens with uncertain micro/macrostructure. Sequential boundary data are used to design an imaging functional that is invariant to (unknown) stationary features of the domain.
-
Extension to highly heterogeneous composites — PRSA, 2023.Extends the differential indicators to randomly heterogeneous composites for exclusive tomography of elastic transformation and fracturing in real-world materials and structures of arbitrary complexity.
-
Laboratory validation via laser vibrometry — MSSP, 2021.First experimental demonstration of the differential evolution indicators; images the fracturing process.
Thrust B: Data-driven modeling and inverse design of advanced materials
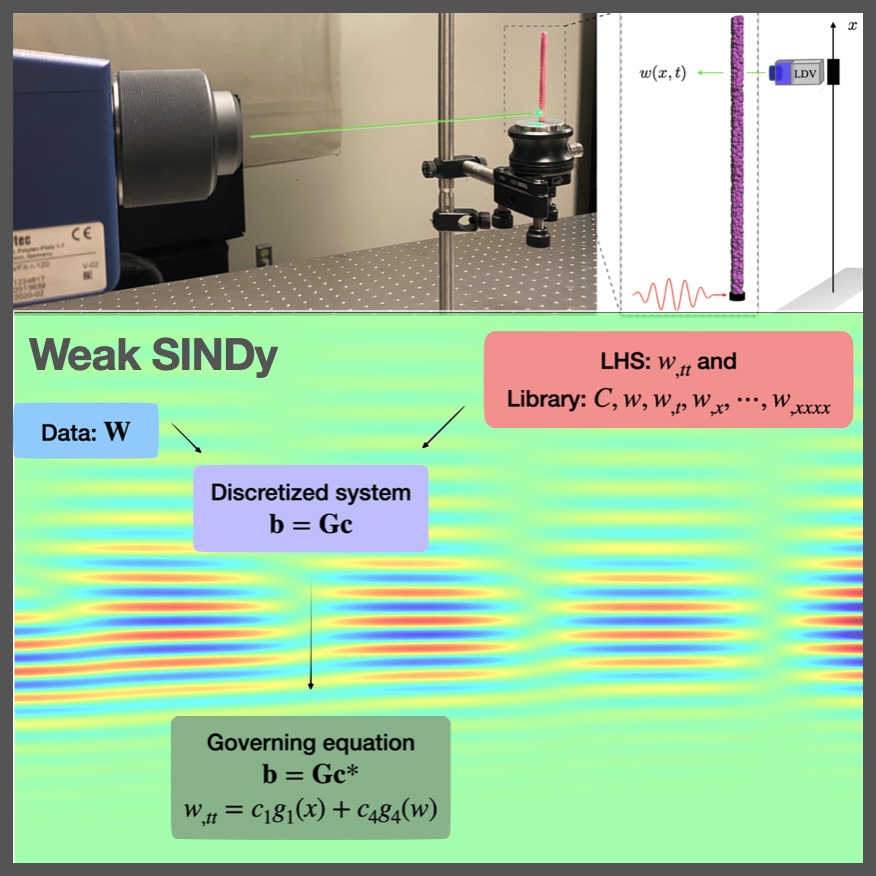
Operator learning on full-field measurements enables data-driven discovery of the mechanics of materials with complex micro–meso–macro structure, especially in dynamic regimes where scale-separated homogenization fails and effective governing equations remain poorly understood. Laser ultrasonics and laser speckle interferometry pave the way by providing high-resolution, full-field measurements across a wide frequency range. We aim to learn and experimentally validate, with quantified uncertainty, the governing operators of hierarchical/particulate materials by: (i) identifying particle-to-continuum laws and closures; (ii) learning a hierarchy-to-dynamics map that remains predictive across scales; and (iii) delivering fast, physics-based surrogates that extrapolate beyond training. These developments enable predictive modeling of advanced materials, such as dense porous foams, metamaterials and metastructures, metallic-powder AM builds, and densely packed particle beds – and facilitate inverse design of next-generation metamaterials that expand achievable dynamics and unlock previously inaccessible functions. Signature results
-
Ensemble WSINDy for experimental PDE discovery — MSSP, 2024 (under revision).Weak-form sparse regression with ensemble UQ on laser vibrometry measurements; Recovers governing PDEs and affiliated parameters for bonded granular specimens at low frequencies.
-
Micropolar Deep Material Networks — CMAME, 2025.Establishes physics-based neuron operators in a binary-tree hierarchical surrogate for micropolar continua, capturing micro-rotations/couple-stresses and microstructure-dependent size effects; Accurately predicts mesoscale homogenized response with runtime far below that of full-field solvers.
-
Deep learning for full-field ultrasonic characterization — MSSP, 2023.Introduces wavenumber-adaptive Sobolev losses and learned regularization for training on highly oscillatory and multi-fidelity measurements. Enables accurate neural characterization of discontinuous and heterogeneous composites from full waveform test data.
Thrust C: Data-driven discovery of interfacial mechanics
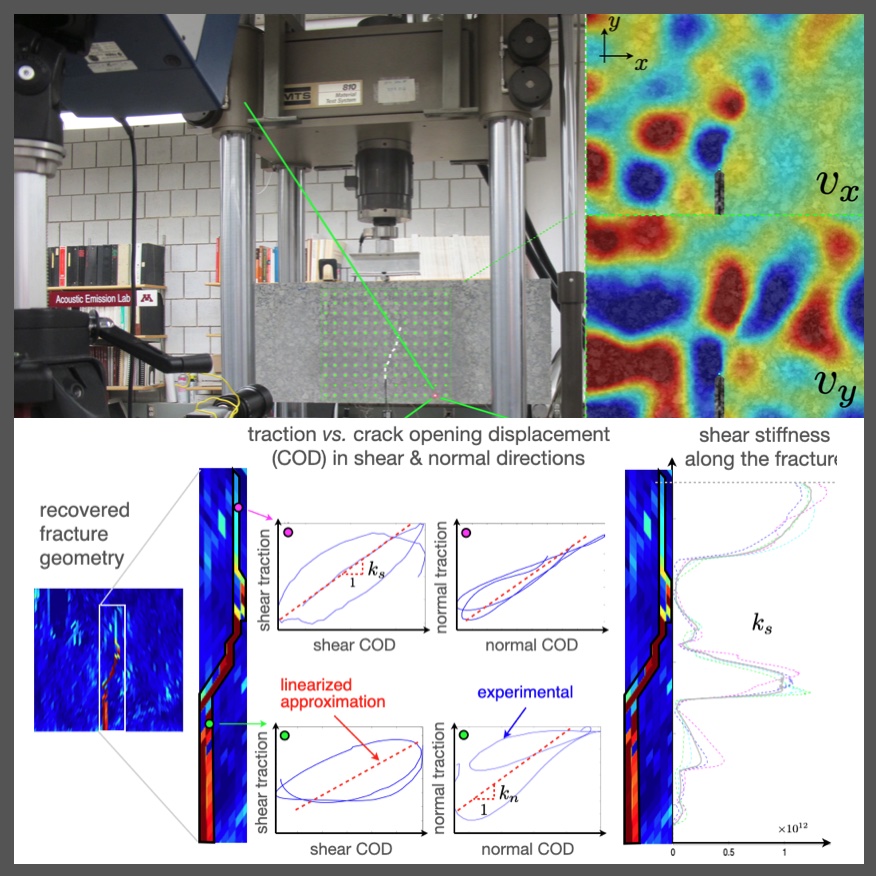
Interface operators govern the behavior of composites, AM bonds, layered builds, and fractured geomaterials, yet remain poorly characterized under realistic loads and bandwidths. Full-field, near-interface measurements enable experimental discovery and validation of multiscale, nonlinear, and rate-dependent behaviors that common contact models miss. We aim to uncover and experimentally validate the governing operators of frictional and cohesive interfaces by: (i) learning the effective traction–separation and rate-and-state slip weakening laws from wideband measurements with quantified uncertainty; and (ii) upscaling roughness and microstructure into effective dynamics across rates and frequencies. These developments enable predictive modeling and control of interfacial and effective-medium behavior in critical materials and energy systems. Signature results
-
On the elastic anatomy of heterogeneous fractures in rock — IJRMMS, 2018.Nonparametric recovery of fracture geometry and heterogeneous shear/normal specific stiffnesses from full-field laser vibrometry data.
-
Nonlinear model identification of a frictional contact support — MSSP, 2010.Identifies nonlinear friction laws and parameters for a contact support via reduced-order system identification; Accurately predicts structural dynamics and hysteretic slip–stick behavior from vibration data.
-
A synoptic approach to the seismic sensing of heterogeneous fractures: From geometric reconstruction to interfacial characterization — CMAME, 2017.A unified, non-iterative pipeline that reconstructs interfacial stiffness from remote data by first performing geometric reconstruction and then inverting boundary-integral equations with proper regularization.
Laser ultrasonics & Laser vibrometry
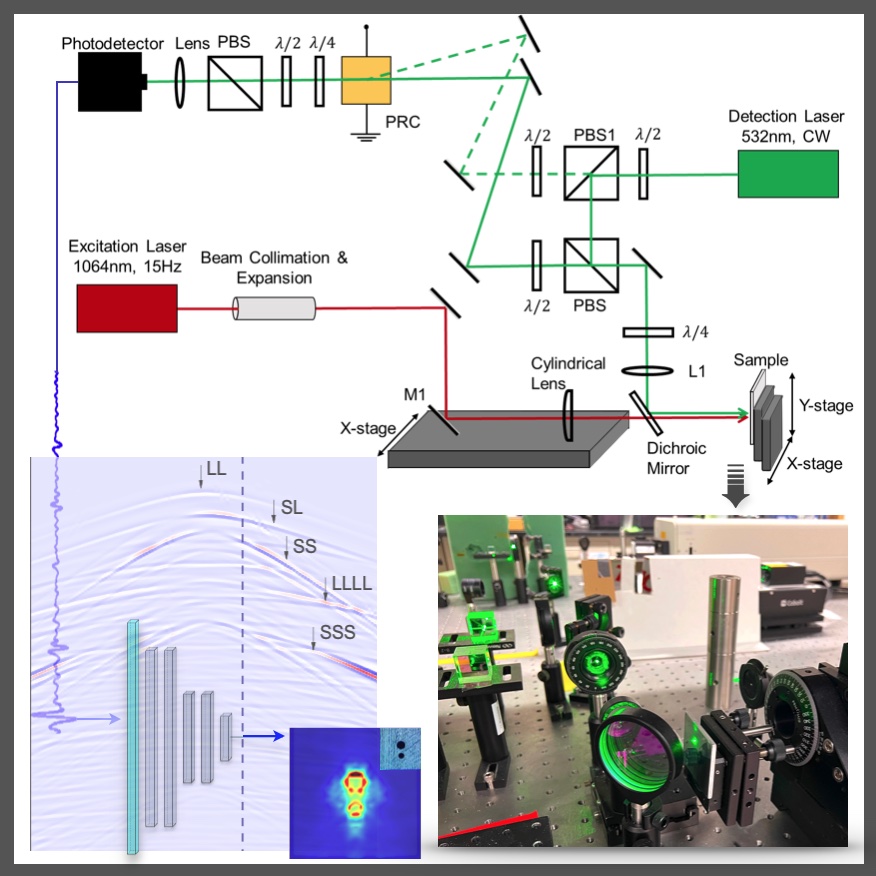
We develop and deploy two types of non-contact, laser-based testing setups: laser ultrasonics (LU), which uses a pulsed laser for broadband ultrasound generation with interferometric detection, and laser Doppler vibrometry (LDV) paired with piezoelectric transducers for excitation. Together, these setups deliver wideband excitation and high-resolution, full-field measurements. The resulting dense spatiotemporal data and repeatable experiments power Thrust A (inverse scattering in complex, uncertain media), Thrust B (operator learning and inverse design), and Thrust C (data-driven discovery of interfacial mechanics). They enable flexible near- and far-field measurements, uncertainty-aware validation, and rapid iteration between models and experiments across rates and frequency ranges. Signature results
-
Laser ultrasonic imaging of subsurface defects with the linear sampling method — Optics Express, 2023.Integrates the multi-frequency LSM indicator into laser ultrasonics and demonstrates state-of-the-art performance by achieving super-resolution and accurate shape reconstruction below the diffraction limit.
Past contributions (as student)
High-frequency inverse scattering via Topological Sensitivity
with: Bojan Guzina
This study deciphers the topological sensitivity (TS) as a tool for shape reconstruction of hidden scatterers from remote data in the high-frequency regime. The TS indicator, expressed as a pair of nested surface integrals, is found to survive upon three asymptotic lynchpins: (i) the near-boundary approximation for sampling points close to the ‘exposed’ surface of an obstacle; (ii) uniform expansions synthesizing the diffraction catastrophes for sampling points near caustic surfaces, lines and points; and (iii) stationary phase approximation. It is then shown that, in the case of the full source aperture, the TS is asymptotically dominated by the (explicit) near-boundary term featuring shape reconstruction capability.
Wave propagation through a rough interface
with: Bojan Guzina and Roman Tokmashev
This study takes the first step toward "imaging" the true contact law along the interface of a heterogeneous fracture. To this end, the spatiotemporal displacement jump across the fracture surface is recovered from laser vibrometry data, together with the affiliated traction vector by way elastography. This enables point-wise characterization of the fracture's contact condition by revealing the underpinning traction-displacement jump relationship and its evolution with time.
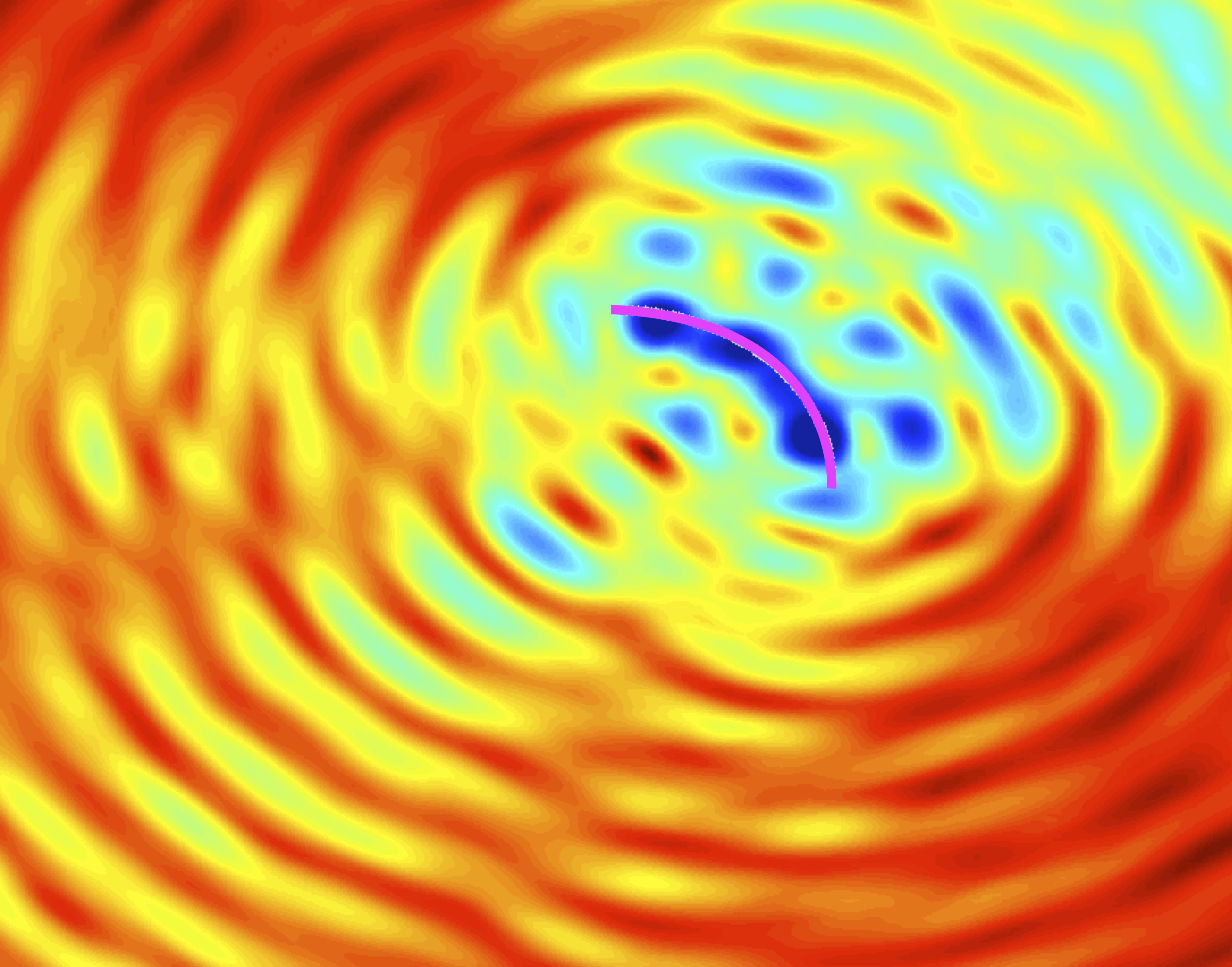 TS reconstruction of a 3D fracture (slides).
TS reconstruction of a 3D fracture (slides).
On the elastic-wave imaging of fractures with interfacial stiffness
with: Bojan Guzina
The TS indicator is extended to enable simultaneous 3D reconstruction of fractures and qualitative characterization of their interface, in low-frequency regimes, by way of elastic waves.
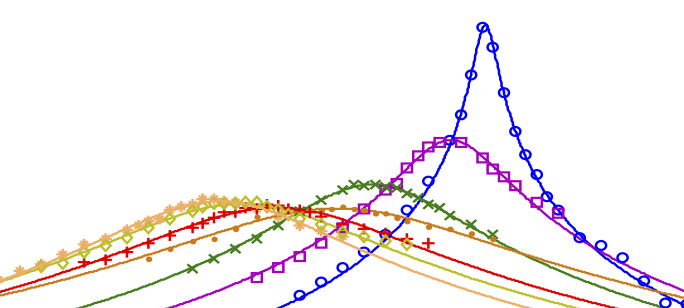 Evolution of the frequency response function affiliated with a nonlinear dynamical system in terms of the amplitude of motion (slides).
Evolution of the frequency response function affiliated with a nonlinear dynamical system in terms of the amplitude of motion (slides).
Experimental reconstruction of Nonlinear Normal Modes
with: Hamid Ahmadian
The concept of Nonlinear Normal Modes (NNMs) is deployed to extend the classical modal analysis to nonlinear systems. We propose two feasible ways to reconstruct NNMs from experimental data: (i) by formulating the equivalent linear model for a nonlinear system in the vicinity of its resonance frequencies such that the affiliated NNMs are identified as the normal modes, and (ii) by taking the motion of a nonlinear system near a resonance frequency as its corresponding NNM. The later is capable of recovering NNMs of complex structures with global nonlinearities and it shown to be effetive for reduced-order system identification.
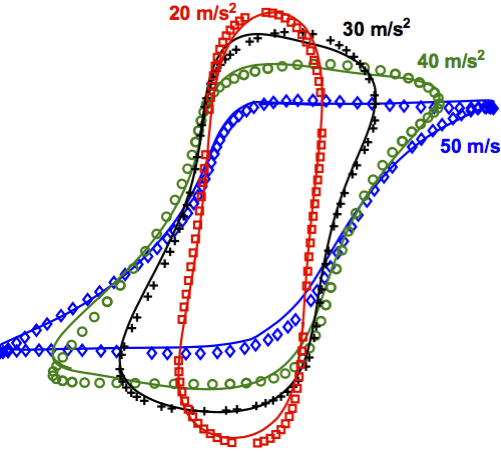 Frictional force vs relative velocity at the interface of a mechanical joint under harmonic excitation (slides).
Frictional force vs relative velocity at the interface of a mechanical joint under harmonic excitation (slides).
Nonlinear model identification of frictional interfaces under micro-vibro- impact and slip
with: Hamid Ahmadian and Hassan Jalali
This study investigates the nonlinear behavior of a frictional contact in situations where micro-impacts develop in the normal direction to the interface. In particular, the effect of (temporally) variable normal load on the frictional forces are studied, and a new interface law is proposed that is capable of taking into account such effects.
